• 也可以叫做 Greedy Algorithm（貪婪演算法）

  • 也是會到達 globally-optimal solutions

  • 只看眼前的狀況，不看整體

  • 可以用貪婪演算法解決的問題 - Job Sequencing with Deadlines

  • 可以用貪婪演算法解決的問題 - Fractional Knapsack Problem

個人想要理解的部分：

  • 基本的定義，什麼樣的概念可以叫做貪婪演算法

  • 什麼地方或是什麼情況會使用到

這篇會整理我所理解及整理的資料。

基本定義

核心是在每一步都只選擇當下最好的選擇，藉由選擇當下看起來最好的選擇，達到最後結果是全域最佳解。

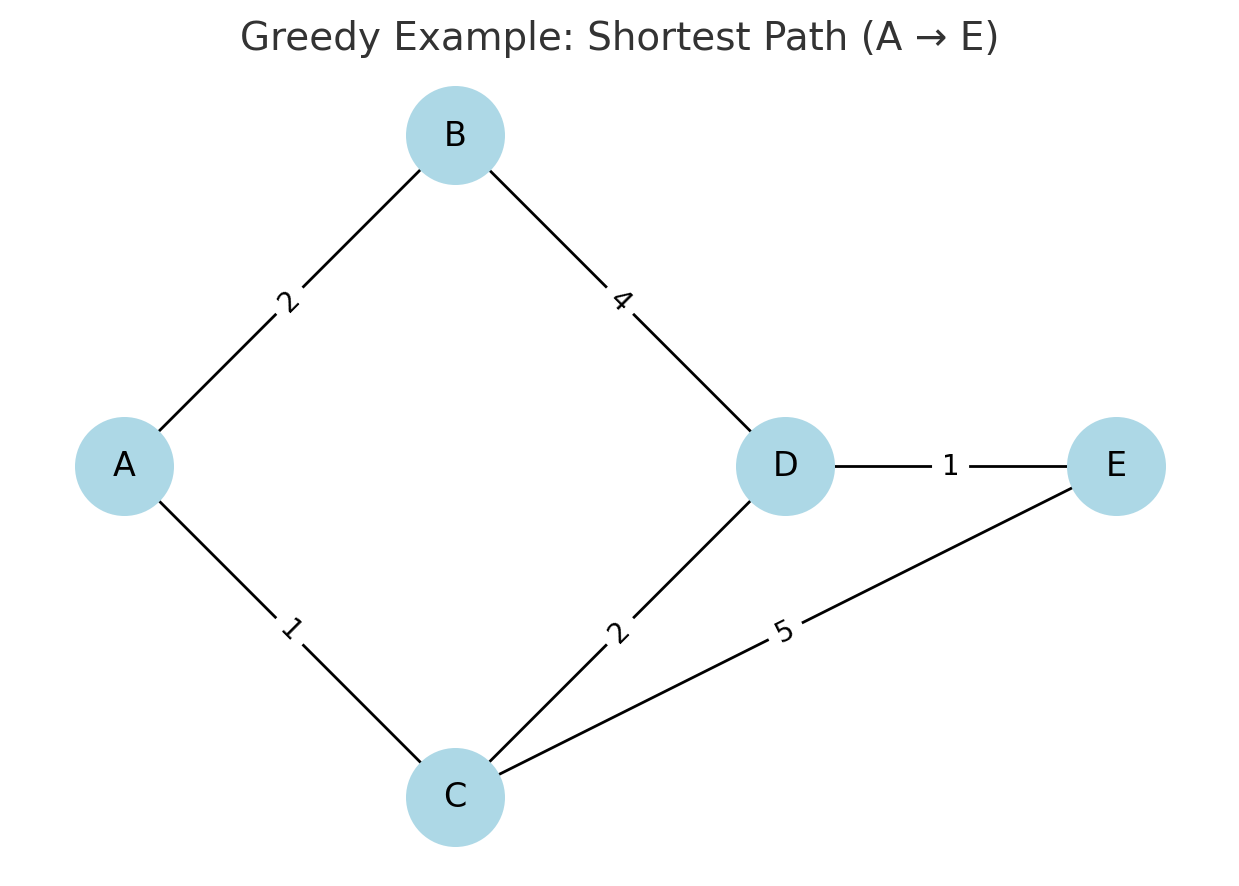
這個圖當作範例：

如果想要找到 A → E 的最短路徑，從 A 出發會先選 1 到 C 因為比 2 小，到 C 後再選 2 到 D 因為比 5 小，最後路徑是 A→C→D→E，長度 4。

這就是所謂透過 Greedy 策略的方式做選擇，但要注意這個圖片的例子剛好最後是最佳解，但使用 Greedy 的不一定都會得到全域最佳解。

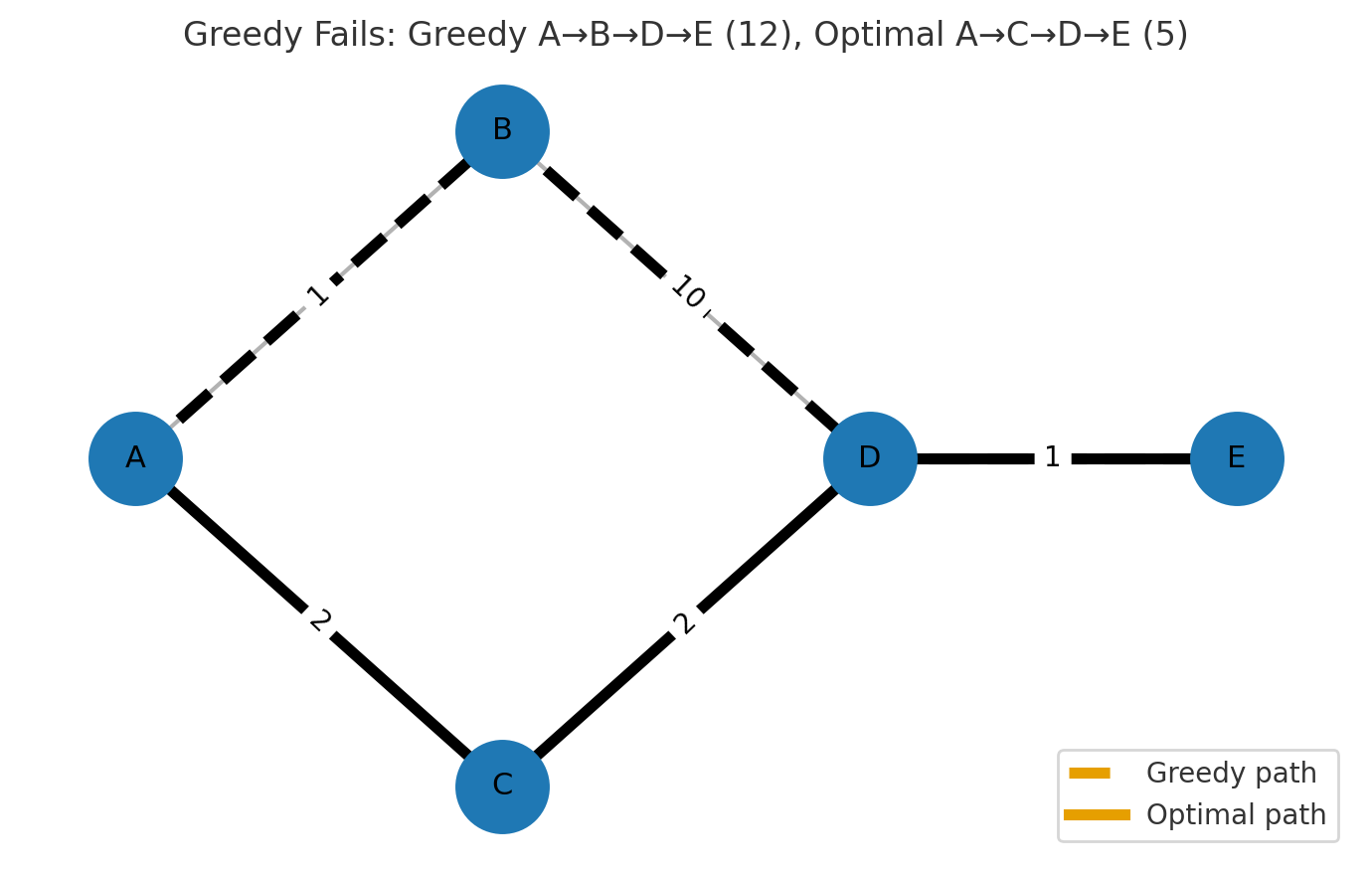
像是這個圖來說：

使用 Greedy 策略的話，A 遇到第一個選擇 1 比 2 小所以會走 B，所以路徑是 A→B→D→E 是 12，

但會發現這並不是最佳解，因為如果走另一個 A→C→D→E 只有 5，有些狀況當下最好的選擇但不是最終最佳的選擇。

回來基本定義這邊。

Greedy 策略還有一個 no backtracking 的特性，也就是一旦做出選擇之後就不會回頭，我今天從 A 基於判斷選擇到 B 之後，就算最後證明那不是最好的，但走都走了就繼續往下去，不會再回到 A。

適合貪婪演算法的問題必須滿足兩個特性，Greedy-choice property 和 Optimal substructure。

Greedy-choice property 意思是如果你每次只選當下「看起來最好」的選擇，最後拼湊起來也能得到整體最好的解。

Optimal substructure 大問題的最佳解，可以分解成小問題的最佳解組合而成。

主要就是要保證兩件事情的前提下，

  1. 保證「只看眼前」也不會走錯。

  2. 保證「小問題的解」能拼湊成「大問題的解」。

接下來看兩個範例後就能更了解。

Job Sequencing with Deadlines

就是每個工作都有截止時間和收益。

這個問題要想辦法找出最好的排法讓效益最高。

貪婪策略的話就會優先選擇收益最高的工作，並盡量排在可行的最晚時間。

看下面這個例子：

1
2
3
4
5
6
| Job | Deadline | Profit |
| --- | -------- | ------ |
| A   | 4        | 70     |
| B   | 1        | 80     |
| C   | 1        | 30     |
| D   | 2        | 100    |

  1. 依收益排序： D(100), B(80), A(70), C(30)

  2. 安排：

    • D → deadline=2 → 安排在第 2 單位時間

    • B → deadline=1 → 安排在第 1 單位時間

    • A → deadline=4 → 安排在第 4 單位時間

    • C → deadline=1 → 已經滿了，跳過

  3. 最後排程：B, D, A

  4. 總收益 = 80 + 100 + 70 = 250

這種思考模式就是種 Greedy 策略，每次先挑收益最高的工作，然後往 deadline 靠近。

因為滿足了 Greedy-choice property ( 先挑最大收益不會錯），跟 Optimal substructure （小子問題最佳解能組合成大解），所以適合用貪婪演算法來解這種類型問題。

Fractional Knapsack Problem

這個問題是要分散背包裡面的東西，環境是背包容量有限，可以分割物品。

貪婪策略的話會依照「單位重量價值」排序，優先放入價值密度最高的物品。

聽說 DP 也能解這種題目，但我還沒看到那邊。

假設背包容量 W=50W = 50W=50，物品如下：

1
2
3
4
5
| Item | Weight | Value | Value/Weight |
| ---- | ------ | ----- | ------------ |
| A    | 10     | 60    | 6.0          |
| B    | 20     | 100   | 5.0          |
| C    | 30     | 120   | 4.0          |

Greedy 解法步驟：

  1. 先放 A (10kg, value=60)

  2. 再放 B (20kg, value=100)

  3. 背包剩餘 20kg → 放 C 的 2/3 (value=80)

總價值 = 60 + 100 + 80 = 240

選擇順序就會為 A → B → C(2/3)，這時候 240 也剛好是最大價值。

結語

可以理解成是一種簡單、效果高但不能保證最佳解的演算法，見一步走一步的思考方式很直覺，邏輯寫起來也不複雜，對於一些「局部最佳 = 全域最佳」的問題是很好的解法。